10 Greatest Contributions Of Srinivasa Ramanujan, Indian Self-Taught Math Genius

Srinivasa Ramanujan was an Indian mathematics genius who had made several major contributions to many fields of math despite receiving little formal education. His contributed for continued fractions, game theory, number theory, mathematical analysis, and infinite series.

He could solve some seemingly unsolvable math problems and some of his works are so ahead of his time that modern mathematicians are still struggling to understand their relevance.

Here are Ramanujan’s ten greatest contributions to mathematics:

Ramanujan's Series Contributed To The Finding Of The Fastest Algorithms To Calculate Pi

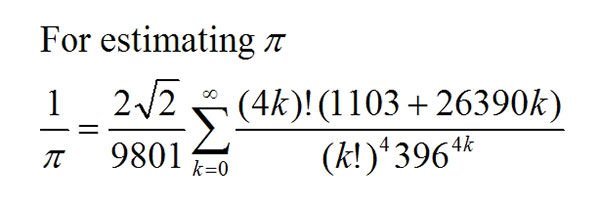
Mathematics has seen only a handful of important challenges that can puzzle generations of mathematicians, and one of them is the approximation of pi (π). Back in 1914, Ramanujan came up with a formula to compute an extra of eight decimal places.

One of Ramanujan’s π infinite series had paved the way for the Chudnovsky brothers’ achievement in 1989 when they computed more than one billion decimal places of pi with the help of a supercomputer.

His series is also the building bricks for the fastest algorithms ever found to calculate pi.

The Ramanujan’s Conjecture Paved The Way For The Development Of Langland Program

In 1916, Srinivasa Ramanujan made public a paper highlighting Fourier coefficients of modular forms’ properties. Back then, the theory for modular forms was not so developed, but his work had served as a beacon for its development.

Two decades after his paper was published, the Hecke theory was formed by Erich Hecke, a German mathematician, on the basis of Ramanujan’s first two conjectures.

However, what makes Ramanujan’s name in the mathematics community of the 20^th century is the last conjecture, which helped a lot with the development of the Langland program, started 1970 by Robert Langland. What the program does is to relate algebraic number theory and representation theory, the two seemingly unrelated fields of mathematics.

So what Ramanujan did changed forever the course of 20th-century mathematics.

He Helped Developed The Circle Method In Partition Number Theory

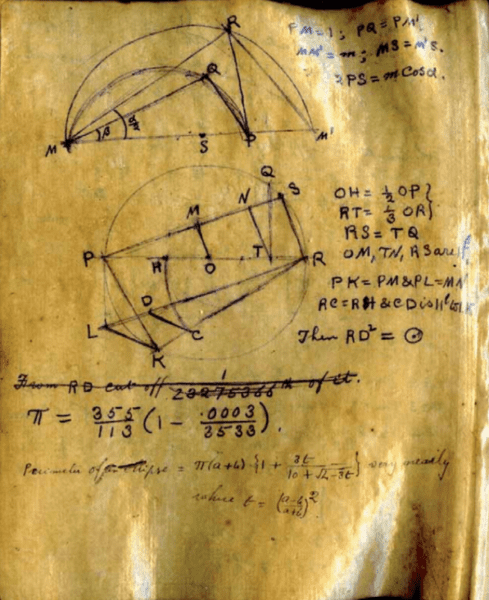
H. Hardy and Ramanujan together found the circle method that allows the calculation of the partition of numbers’ first approximations beyond 200.

This is the method that contributed greatly to the advancement of challenging math problems, like the Waring’s conjecture. It is also one of the most important tools in analytic number theory.

He Discovered Three Ramanujan’s Congruences

Another achievement of Ramanujan is the three partition function p(n)’s congruences. He was so ahead of his time that it was not until 2011 that a conceptual explanation for his congruences was published.

His contributions in partition theory are the basis for modern probability and particle physics.

The Hardy–Ramanujan Number

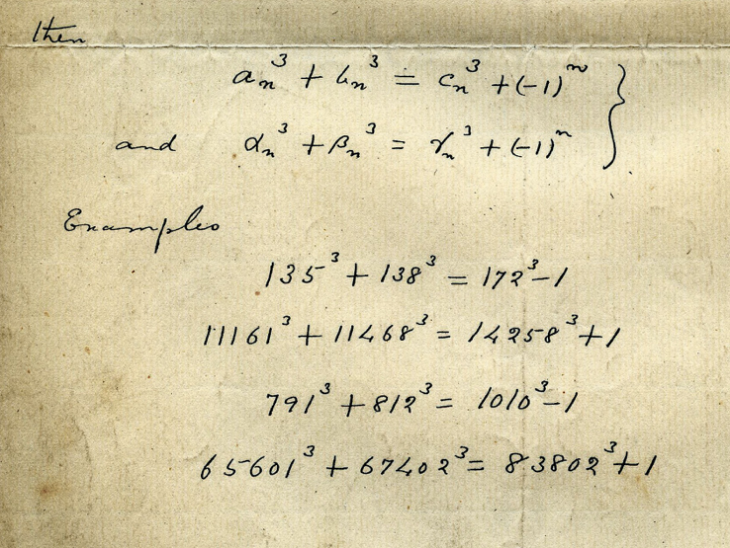
H. Hardy in a visit to Ramanujan rode a taxi numbered 1729. Later, when the British mathematician shared this incident with the Indian genius, Ramanujan found out that the number 1729 is the smallest that can be expressed as the sum of two cubes in two ways. 1729 is part of a theorem the Indian mathematician was developing. It is relevant to the theory of elliptic curves.

His Research Helped Proving Fermat’s Last Theorem

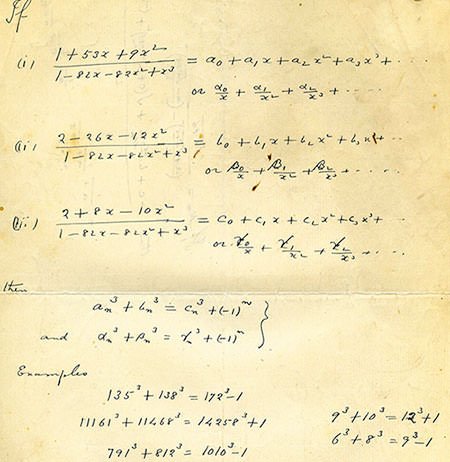
Back in 2013, Sarah Trebat-Leder and Ken Ono found out that the Indian mathematician was working on Fermat’s last theorem, one of the most challenging problems in the history of mathematics.

If the points of his equation are plotted, we will have an elliptic curve, which played a vital part in Sir Andrew Wiles’s answer that proved Fermat’s last theorem in 1994.

Ramanujan Was The First Mathematician To Found Out About The K3 Surfaces In The 1910s

Elliptic curves are not the most complicated object Ramanujan had ever researched. In 1958, when one of his objects was re-discovered by Andre Weil, it got the name the K3 surface. And the Indian mathematician’s work had shown some of its features that did not know to mathematicians before.

That is not all. Without the K3 surface, we would not have today’s quantum physics and string theory, which suggests that the world is more than the three dimensions that humans can see. The rest of the dimensions are packed in minus spaces, which have a distinctive geometric structure, that we cannot see with our bare eyes.

His Theta Function Is The Heart Of String Theory Of Physics

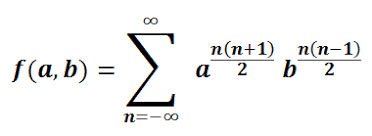
Theta functions consist of several complex variables. Carl Gustav Jacob Jacobi came up with several of them and they are called Jacobi theta functions.

Ramanujan also researched the theta function and came up with his own, which contains the general properties of those of Jacobi but at the same time, generalizes them.

His theta function has numerous practical applications, including determining superstring theory’s, M-theory’s, Bosonic string theory’s critical dimensions.

HIS MOCK MODULAR FORMS MAY UNLOCK THE SECRET OF BLACK HOLES

In a letter he wrote for Hardy, Ramanujan talked about numerous functions that mimic the known modular forms or theta functions, but behave in different ways. These functions served as the first mock modular forms’ examples.

He also predicted that the mock modular forms and ordinary modular forms’ correspondence would produce much the same roots of 1’s outputs.

Mock modular forms’ expansion has contributed greatly in computing the level of disorder, black holes, or the entropy.

Back then, back holes were a strange concept but the Indian mathematician was able to come up with maths that can help us reveal their best-kept secrets.

>>> Indian Mathematician Srinivasa Ramanujan And His Famous Quotes